计算几何算法2. 关于线和点到线的距离（二维和三维）

关于直线
直线方程
点到直线的距离
用两点表示的直线
2d隐式表示的直线的情形
参数方程表示的直线
一个点到射线或线段的距离
代码实现

距离计算是计算机图形学和计算几何的基本问题，而且有很多关于这方面的公式。不过，由于对象描述方式不同，有替代方案可供选择。我们将说明其中的一些情况。

自始至终，我们需要有一个度量来计算两点之间的距离。我们假定有基于毕达哥拉斯定理的欧几里德度量标准。也就是说，对于一个n维向量v =（用V₁，V₂ ,…,V_n），其长度| v |由下式给出：

clip_image002

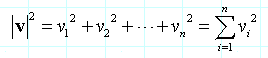
而两点P值（的p₁，p₂ ,…, p_n）和Q =（q₁，q₂及,…, q_n），它们之间的距离是：

clip_image004

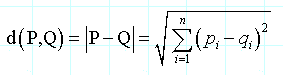
关于直线：

定义直线L是通过给两个不同的点P₀和 P₁来定义的。事实上，它定义了一条从P₀至P₁的线段，这是古希腊人理解直线的方式，它与我们所知道的两个端点之间的最短路径的自然直觉相吻合。直线可以向两端无限地延长，这就是我们今天经常提到的直线的概念。不过，对于古希腊人，线是可以无限延长的有限线段。这种定义方式的好处是，它适用于所有维度：二维，三维，或任何n维空间。而且，一般在实际应用中通过端点来定义一条线段，因为线段一般用来表示多边形、多面体或内嵌图形的边。

直线L也可以通过一个点和一个方向来定义。让P₀是直线L上的一点，v_L是表示直线方向的非零向量。这个方法等价于直线的两点定义的方式，由于可以把v_L=（P₁-P₀）。或者给定P₀和v_L，可以选择P₁=P₀+v_L 作为直线的第二个点。如果v_L被归一化为方向的单位向量，u_L=v_L/|v_L|，那么它的元素就是直线L的方向余弦。也就是说，在n 维，让q_i (i=1,n)是直线L和第i个轴a_i的角度（例如，在2D，a₁是在x轴和a₂是y轴）。那么，向量v_L = (v_i)，有v_i = cos(q_i)是直线L的方向向量。在2d如下图所示，如果q 是直线L与x轴的角度，那么cos(q₂) = sin(q)，即v_L = (cos(q₁), cos(q₂)) = (cos(q), sin(q)) 是L的单位方向向量，因为：cos²(q) + sin²(q) = 1。同样，在任意维度上，方向余弦的平方和为1，即：S cos²(q_i) = 1。

clip_image006

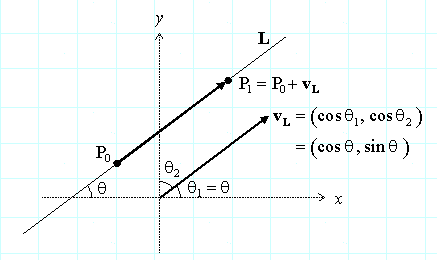
直线方程：

直线也可以定义为为未知方向上的点坐标方程。以下是一个在实践中通常遇到方程式：

类型	方程式	使用
2d显式的表示方法	y = f(x) = mx+b	非垂直的2d直线
2d隐式的表示方法	f(x,y) = ax + by + c = 0	任意2d直线
参数方法	P(t) = P₀ + tv_L	任意维度的任意直线

2d显式的表示方法是在中学讲过的，但它不是最灵活的方法。2d隐式的表示方法是较为有效的，显式方法转换为隐式方法是容易实现的。通常使用隐式方法的两个参数定义一个向量n_L=(a,b)，它垂直于直线L。这是因为直线L上任意两点P₀=(x₀,y₀) 和 P₁=(x₁,y₁)，我们有n_L·v_L = (a,b)·(P₁-P₀) = a(x₁–x₀) + b(y₁–y₀) = f(P₁) – f(P₀) = 0。因此，我们说n_L是直线L的单位向量，意味着垂直于直线L。而且，给定任意直线的法向量n_L=(a,b)和一个直线上任意一点P₀，隐式方程的法线形式是：

clip_image008

这个方程如果a² + b² = 1则是归一化的，从而n_L是单位法向量，常常用u_L表示。

不幸的是，一个隐式（或显式）方程仅仅能够定义一条2d直线，而在3d中直线方程定义了一个平面，在n维空间中它定义了一个n-1维的超平面。

另一方面，在任意n维空间，直线的参数方程是有效的，也是最通用的一种表示方法。通过两个点P0和P1、方向向量v_L来定义一条直线，即：

clip_image010

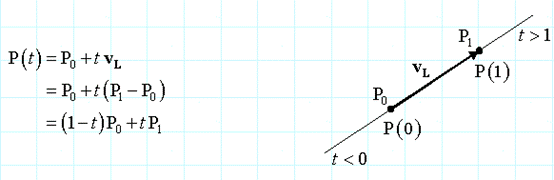
其中t是一个实数。其中P(0)=P₀，P(1)= P₁。P(t) 有 0<t<1 表示P₀和P₁之间的线段，其中t是分数。也就是说，t = d(P₀,P(t)) / d(P₀,P₁)，因此，P(1/2)=(P₀+P₁)/2 是线段的中点。而且，如果t <0，则P(t)位于P₀方向的外侧，如果t >1，则P(t)位于P₁方向的外侧。

我们可以方便地从一种表示方法向另一种表示方法转换。例如，给定两个直线上的点P₀=(x₀,y₀) 和 P₁=(x₁,y₁) ，可以推导出它的隐式方程，即通过v_L=(x_v,y_v)=P₁-P₀=(x₁–x₀, y₁–y₀)，我们有n_L=(-y_v,x_v)=(y₀–y₁,x₁–x₀) 是垂直于直线L的法向量。因为 n_L·v_L= 0，直线L的隐式方程为：

其中x和y的系数是n_L的组成部分。

另外，在2d，如果直线L与x轴的角度为q，回忆一下即v_L = (cos(q), sin(q)) 是单位方向向量，那么n_L = (-sin(q), cos(q)) 是单位法向量。所以如果P₀=(x₀,y₀)是直线L上一点，那么直线L归一化的隐式方程为：

因为sin²(q) + cos²(q) = 1。参数方程是：

clip_image016

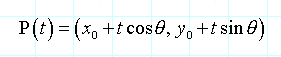
点到直线的距离：

给定一条线L和一个点P，让d(P,L) 表示点P到直线L的距离，这是P到直线L的最短距离，假如L是一条无限延伸的直线，那么这是一个从点P到直线L的垂线。但是如果直线L是一条有限长度的线段S，那么垂线的底可能超出线段，这是计算最短距离需要考虑一些其他的因素。我们首先考虑点到无限延伸的直线的垂直距离。

用两点表示的直线：

在2d和3d中，直线L是由两个点P₀和 P₁确定，可以使用叉乘直接计算从任意一点P到直线L的距离。2d情况可以作为z轴等于0的特例来处理。关键的发现是两个3d向量的叉乘等于由它们围起来的平行四边形的面积，既然|v×w| = |v| |w| |sinq | ，其中q 是两个向量v和w之间的夹角。同时，平行四边形的面积还等于底乘以高，我们把高定义为d(P,L)。v_L=P₀P₁=(P₁-P₀) 和w=P₀P=(P-P₀)，如图：

clip_image018

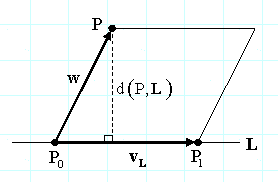
那么，|v_L× w| = Area(平行四边形(v_L,w) ) = |v_L| d(P,L)的结果为：

clip_image020

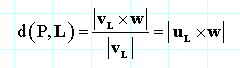
其中u_L= v_L / |v_L| 是直线L的单位方向向量，如果需要计算许多个点到一条直线的距离，首先计算 u_L是最有效的方式。

对于内嵌到3d空间的2d情况，点P=(x,y,0)，叉乘为：

clip_image022

和距离计算公式为：

clip_image024

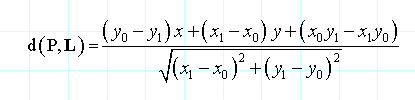
2d隐式表示的直线的情形：

在2d，直线L是定义为隐式方程f(x,y) = ax+by+c = 0。对于任意2d点P=(x,y)，距离d(P,L)可以利用这个方程来直接计算。

回忆一下，向量n_L = (a,b)垂直于直线L。利用n_L可以计算任意点P到直线L的距离。手续ian选择直线L上任意点P0，然后做P₀P到n_L的垂线，如下图所示：

clip_image026

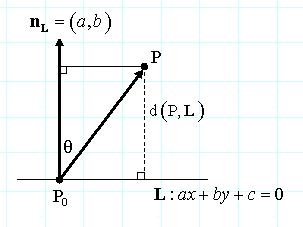
我们有：
（1）由于a和b不能同时为零，假设一个a!=0，并选择直线上点P₀=(-c/a,0)， [否则，若a = 0而b != 0，选择P₀=(0,-c/b)，具有同样的结果]
（2）对于任意直线L上的点P₀我们有：n_L · P₀P = |n_L| |P₀P| cos q = |n_L| d(P,L)
（3）对于我们指定的P₀： n_L ·P₀P = (a,b) · (x+c/a, y) = ax+c+by = f(x,y) = f(P)
结合（2）和（3）得出公式如下：

clip_image028

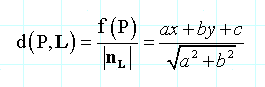
而且，我们可以在|n_L|上除以f(x,y)的系数而预先归一化方程，使 |n_L|=1。就会得到非常有效率的公式：

clip_image030

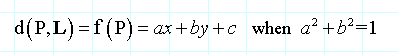
其中对于每次的距离计算只有2次乘法和2次加法。因此，如果需要计算二维多点到直线L的距离，那么应该计算单位法向量来使用这个公式。另外请注意，如果只是比较距离（例如，需要寻找距离直线最近或最远的点），那么归一化是没有必要，因为它只是改变了一个常数因子。

回忆以下，有直线L，做直线L与x轴的夹角q 和直线上任意点 P₀=(x₀,y₀)，然后归一化的隐式方程有：a = -sin(q), b = cos(q), c = sin(q)x₀ -cos(q)y₀.

参数方程表示的直线：

为了计算任意维度空间从任意点P到直线L的距离d(P,L)，直线L的方程由参数方程给出。假设P(b)为点P到直线L的垂足。那么直线有参数方程给出：P(t)=P₀ + t (P₁-P₀)。那么向量P₀P(b)是向量P₀P在线段P₀P₁上的投影，如图所示：

clip_image032

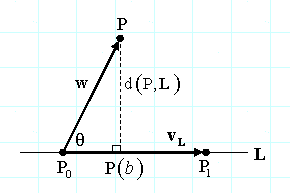
因此，通过v_L=(P₁-P₀)和w=(P-P₀)，有：

clip_image034

clip_image036

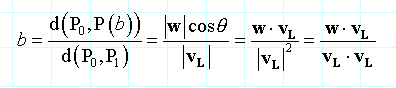
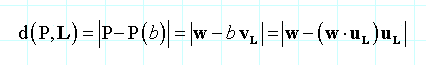
这里u_L是直线的单位方向向量。这个公式的优势是：可以工作在任意维度上，有时候计算垂足P(b)也是有用的。在3D中叉乘公式是更有效率的。在2D当不需要P(b)时，隐式的公式更好，特别是计算多点到同一直线的距离的时候。

一个点到射线或线段的距离

射线R是从点P₀开始向某一方向无限延伸。它可以使用参数方程表示为P(t)，其中t>=0有起点P₀。线段S有两个端点P₀和P₁，使用参数方程表示为P(0)=P₀ 和P(1)=P₁ ，P(t)有 0<=t<=1。

计算任意点P到射线R和线段S的距离和计算任意点P到直线L的距离之间的差异在于：从点P到直线L的垂足P(b)有可能位于射线R或线段S之外，在这种情况下，实际的最短距离是点P到射线R的起点P₀或是到线段S的两个端点之一的距离。

clip_image038

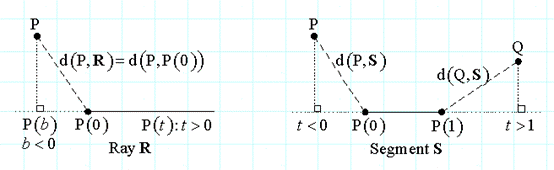
对于射线只有一种选择。但对于线段S而言必须确定哪个端点距离点P最近，我们可以计算两个端点到点P的距离，然后使用最短的那个，但这不是最有效率的办法。我们首先确定点P的垂足位于线段S之外，一个容易的做法是考虑线段P0P或P1P和线段P0P1之间的角度。如果任意角度是90度，那么P(b)是对应的端点。如果不是90度，那么看它们是锐角还是钝角。可以通过点积的方法来进行测试。这个结果决定应该使用哪个端点来计算距离，或者计算点P到线段S的垂直距离本身。它可以工作在n为空间：

clip_image040

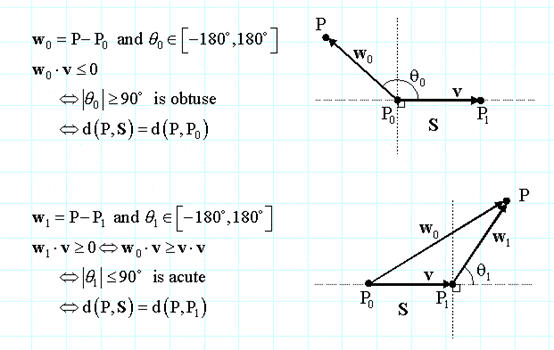
既然w₀= v + w₁，两次测试的结果w₀·v和v·v实际是距离计算公式的分子和分母，通过预先保留计算结果从而提高算法的效率：

distance( Point P,  Segment P0:P1 )
{
       v = P1 - P0
       w = P - P0

       if ( (c1 = w•v) &lt;= 0 )  // before P0
               return d(P, P0)
       if ( (c2 = v•v) &lt;= c1 ) // after P1
               return d(P, P1)

       b = c1 / c2
       Pb = P0 + bv
       return d(P, Pb)
}

然而，在二维情况下，如果我们需要计算从多点到射线或线段的距离，使用规范化方程式做是否一点P有一个新的最小距离的初步测试从L会更加有效；在实践中，一个特定的应用细节将决定哪些是最有效的方法。

代码实现

// Copyright 2001, softSurfer (www.softsurfer.com)
// This code may be freely used and modified for any purpose
// providing that this copyright notice is included with it.
// SoftSurfer makes no warranty for this code, and cannot be held
// liable for any real or imagined damage resulting from its use.
// Users of this code must verify correctness for their application.

// Assume that classes are already given for the objects:
//    Point and Vector with
//        coordinates {float x, y, z;} (z=0 for 2D)
//        appropriate operators for:
//            Point  = Point ± Vector
//            Vector = Point - Point
//            Vector = Scalar * Vector
//    Line with defining endpoints {Point P0, P1;}
//    Segment with defining endpoints {Point P0, P1;}
//===================================================================
// dot product (3D) which allows vector operations in arguments
#define dot(u,v)   ((u).x * (v).x + (u).y * (v).y + (u).z * (v).z)
#define norm(v)    sqrt(dot(v,v))  // norm = length of vector
#define d(u,v)     norm(u-v)       // distance = norm of difference

// closest2D_Point_to_Line(): finds the closest 2D Point to a Line
//    Input:  an array P[] of n points, and a Line L
//    Return: the index i of the Point P[i] closest to L
int
closest2D_Point_to_Line( Point P[], int n, Line L)
{
    // Get coefficients of the implicit line equation.
    // Do NOT normalize since scaling by a constant
    // is irrelevant for just comparing distances.
    float a = L.P0.y - L.P1.y;
    float b = L.P1.x - L.P0.x;
    float c = L.P0.x * L.P1.y - L.P1.x * L.P0.y;

    // initialize min index and distance to P[0]
    int mi = 0;
    float min = a * P[0].x + b * P[0].y + c;
    if (min < 0) min = -min;    // absolute value

    // loop through Point array testing for min distance to L
    for (i=1; i<n; i++) {
        // just use dist squared (sqrt not needed for comparison)
        float dist = a * P[i].x + b * P[i].y + c;
        if (dist < 0) dist = -dist;   // absolute value
        if (dist < min) {    // this point is closer
            mi = i;          // so have a new minimum
            min = dist;
        }
    }
    return mi;    // the index of the closest Point P[mi]
}
//===================================================================
//dist_Point_to_Line(): get the distance of a point to a line.
//    Input:  a Point P and a Line L (in any dimension)
//    Return: the shortest distance from P to L
float
dist_Point_to_Line( Point P, Line L)
{
    Vector v = L.P1 - L.P0;
    Vector w = P - L.P0;

    double c1 = dot(w,v);
    double c2 = dot(v,v);
    double b = c1 / c2;

    Point Pb = L.P0 + b * v;
    return d(P, Pb);
}
//===================================================================
//dist_Point_to_Segment(): get the distance of a point to a segment.
//    Input:  a Point P and a Segment S (in any dimension)
//    Return: the shortest distance from P to S
float
dist_Point_to_Segment( Point P, Segment S)
{
    Vector v = S.P1 - S.P0;
    Vector w = P - S.P0;

    double c1 = dot(w,v);
    if ( c1 <= 0 )
        return d(P, S.P0);

    double c2 = dot(v,v);
    if ( c2 <= c1 )
        return d(P, S.P1);

    double b = c1 / c2;
    Point Pb = S.P0 + b * v;
    return d(P, Pb);
}
//===================================================================

参考文献

David Eberly, “Distance Between Point and Line, Ray, or Line Segment”, Magic Software
Euclid, The Elements, Alexandria (300 BC)
Andrew Hanson, “Geometry for N-Dimensional Graphics” in Graphics Gems IV (1994)
Thomas Heath, The Thirteen Books of Euclid’s Elements, Vol 1 (Books I and II) (1956)
Jack Morrison, “The Distance from a Point to a Line”, in Graphics Gems II (1994)

分享&收藏

转载请注明：陈童的博客 » 计算几何算法2. 关于线和点到线的距离（二维和三维）