• 计算几何算法1. 三角形和多边形的面积（2D及3D）
• 计算几何算法2. 关于线和点到线的距离（二维和三维）
• 计算几何算法3. 包含于多边形内的点的快速绕数
• 计算几何算法4. 关于平面以及点到平面的距离
• 计算几何算法5. 直线、线段和平面相交（2D和3D）

直线和线段相交
平面相交
直线-平面相交
两平面相交
三个平面相交
实现
intersect2D_2Segments()
inSegment()
intersect3D_SegmentPlane()
intersect3D_2Planes()
参考文献

几何图元的相交是许多计算机图形学和建模应用中的重要组成部分。在这里我们来看一下最简单的 2D 和 3D 线性图元：直线、线段和平面的算法。

直线和线段相交

为了计算2D和3D中直线和线段的相交点，使用参数方程表示法是最好的。其它表示法在《计算几何算法2. 关于线和点到线的距离》一节中已经讨论过。本节研究如何从其它表示法转换到参数表示法。

在任意维度中，由两点P₀、P₁定义的直线参数方程式，当参数s为实数且u=P₁-P₀为直线的方向向量时可以表示为

P(s) = P₀ + s (P₁-P₀) = P₀ + s u,

当P(s)是有限线段P₀P₁上的一个点且0<s<1时，用表达式P(0)=P₀， P(1)=P₁，s = d(P₀,P(s)) / d(P₀,P₁). 更进一步， 如果s<0，P(s)在线段P₀之外，如果if s>1，P(s) 在线段P₁的外侧。

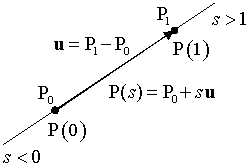
让两条直线满足方程：P(s) = P₀ + s (P₁-P₀) 和 Q(t) = Q₀ + t (Q₁-Q₀)，它们中的一条或者全部是有限线段或者射线。当且仅当方向共线时，直线平行，也就是说当两个向量u=P₁-P₀ 和v=Q₁-Q₀ 成线性关系时，即u=Cv，C为实数。 对于u=(u_k)和v=(v_k)，t意味着所有比值u_k/v_k 相等，或者对于所有的k，u₁/v₁=u_k/v_k 都成立，这等同于所有满足u₁v_k-u_kv₁=0的情况。在2D中，对于u=(u₁,u₂) 和v=(v₁,v₂)，u^⊥· v = u₁v₂-u₂v₁ = 0 这里u^⊥=(-u₂,u₁)垂直于u（⊥称为正交运算符）。。这种情况说明在欧几里得平面上当两条都垂直于相同的方向向量u^⊥时，两条直线是平行的。当这种情况成立时，两条直线既不重合也不相交。

通过验证点P0是否同时在直线和另外一条直线Q(t)上就可以很容易的验证两条直线是否重合。也就是说，存在一个参数t₀ 使等式P₀=Q(t₀)=Q₀+t₀v成立。如果w=(w_k)=P₀-Q₀，对于某个参数t₀存在等式w=t₀v，等同于对于任意的参数k 存在等式w₁v_k-w_kv₁=0。在2D中，这是正交运算情况：w^⊥· v = w₁v₂-w₂v₁ = 0。如果这些条件成立，可以解出参数t₀的值，和无限的直线式重合的。如果一条直线（而不是其它）是一条有限线段，它们重合相交。然而，如果两条直线都是有限线段，它们就可能重叠也可能不重叠。在这种情况下，解出t₀和t₁ 的值使得满足条件 P₀=Q(t₀) 和P₁=Q(t₁)。如果线段区间[t₀, t₁] 和[0,1]不相交，直线就不相交。否则，对区间进行相交运算得出[r₀, r₁] = [t₀, t₁] ∩ [0,1]。相交线段就是Q(r₀)Q(r₁) = P₀P₁ ∩Q₀Q₁。这在任何维度空间里都成立。

当两条直线不平行时，它们可能相交于特殊的一点。在2D欧几里得空间，它们总会相交。在更高维度，它们可能彼此错过不相交。但是如果它们的确相交，它们在2D平面上的线性投影也会相交。所以，一条线段简单的约束到两个坐标点（u 或者v不为0），通过P(s_I)和Q(t_I)计算出2D相交点，然后验证是否P(s_I)=Q(t_I) 对所有的坐标点都成立。为了计算出2D相交点I=P(s_I)=Q(t_I)，考虑如下图中的两条直线和相关向量：

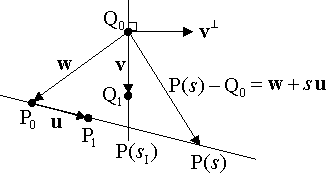
为了确定s_I，在w=P₀-Q₀的情况下，我们得出向量等式P(s)-Q₀ = w + su。在相交点，向量 P(s)-Q₀ 垂直于v^⊥，这等同于v^⊥· (w+su) = 0。求解等式，我们得到：

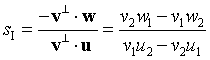
注意，只有像之前讨论过的直线平行时，v^⊥· u = 0。相似地，求解Q(t_I)，我们得出：

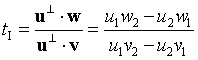
当u^⊥· v = – v^⊥· u时，分母和标志相同，只有在我们想同时知道s_I 和 t_I时，才计算分母。

如果两条直线中的一条是有限线段（或是一条射线），设为P₀P₁，然后当且仅当0<=s_I<=1 （或对于射线有 s_I>=0）时相交点在线段的内部。如果两条线都为有限线段，就要求解出参数s_I 和 t_I，它们都必须在区间[0,1]之间，线段才有可能相交。尽管这听起来足够简单，但是两条线段相交的代码需要一些技巧，因为有很多特殊的情况需要验证（参见我们的2D线段相交实现例子）。

平面相交

平面相交的情况已经在《计算几何算法4. 关于平面以及点到平面的距离》一节中描述过了。

直线–平面相交

在3D中，直线 L或者平行于平面π或者与平面π相交于一点。假设 L满足下列参数方程 P(s) = P₀ + s(P₁-P₀) = P₀ + su，给定点V₀在平面p上，法向量为 n。我们首先检查L是否平行于平面π，如果n·u=0，那就意味着直线法向量 u垂直于平面法向量n。如果成立，直线 L和平面π平行，即或者不相交，或者完全在平面p内。通过验证L上是否存在点P在平面π内，可以判断L和平面π是否相交，也就是说是否满足隐式直线方程：n·(P-V₀) = 0。

如果直线和平面不平行，即直线L和平面π相交于点P(s_I)，利用类似于2D中两条直线相交的方法，我们可以计算出点P(s_I)的值。如图所示：

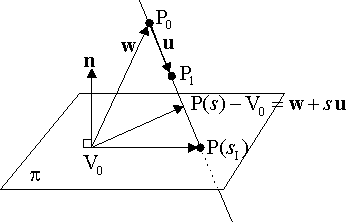
在相交点，当w=P₀-V₀，向量P(s)-V₀ = w+su垂直于n。这等同于点乘：n · (w+su) = 0。求解得出：

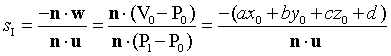
如果L 是从P₀到P₁的有限线段，我们必须检查s_I是否满足 0<= s_I <=1，从而证明线段和平面是否相交。对于正方向的射线，当s_I >=0时，和平面相交。

两平面相交

在3D中，两平面 π₁和π₂或者平行或者相交于直线L。假设 π_i (i=1,2)是由点V_i 和法向量n_i所确定, 满足方程：n_i · P + d_i = 0。只要平面π₁和π₂的法向量平行，它们就平行，等同于n₁×n₂ = 0。在软件中，我们经常用是否|n₁×n₂| < δ当除以δ时是否引起溢出，这是判断 n₁ 和 n₂ 是否平行的条件。如果不平行的话，u = n₁×n₂ >= δ > 0 是相交直线L的方向向量，因为 u 同时垂直于n₁ 和 n₂，也就如图中所示的那样平行于两个平面。 如果 |u| 是个小数，最好将它缩放至|u| = 1，以保证u是单位方向向量。

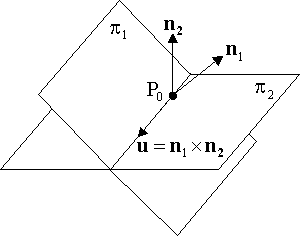
在计算n₁×n₂ (3次相加和6次相乘)后，为了完全确定相交直线，我们仍然需要在上面找到一个特殊点；也就是说，我们需要找到同时在两平面上的点P₀=(x₀,y₀,z₀)。我们可以通过求解关于p₁和p₂的隐式方程来得到P₀。但是这只有两个方程，却需要求解3个未知数，既然点P₀ 能够在任意用于其它自由度的一维直线L上，所以我们需要另外一个条件来求解出点P0。有以下几种方法可以做到这一点：

（A）直接使用线性方程。将其中一坐标点设为0，即为z₀=0，然后解出另外两个点。但是这只在L和平面z₀=0相交时适用。当u =(u_x,u_y,u_z)中的z值不为0时为真。所以，我们必须选择u的非零坐标点，然后设P₀ = 0。我们应该选择拥有最大绝对值的坐标点，因为这会是最健壮的。如果u_z != 0，P₀=(x₀,y₀,0)在L上。求解两方程：a₁x₀+b₁y₀+d₁=0 和a₂x₀+b₂y₀+d₂=0，得出：

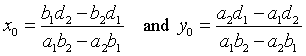
还有L的参数方程：

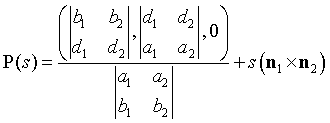
这里的分母和u非零的第三个坐标点是相等的。所以，忽视对非零坐标点的验证，这次求解的所有运算等于有5次相加和12次相乘。

（B）直线相交点。如果知道平面上一条特定的直线（例如，平面上的两个点），和这条直线和其他平面相交，那么相交点”I”同时位于两个平面上。如此，这个点就位于两平面相交线上，L 的参数方程可以表示为：P(s) = I + s (n₁×n₂)。为了计算n1×n2和相交点（给定直线的），我们要进行11次加法运算和19次乘法运算。

在平面内构建一条和其他平面相交的直线的一种方法是，将此平面的法向量投射到另外一个平面上。给定一条直线，令其始终垂直于两平面的相交线。因此，n₂在平面π₁上的投影确定了和π₂相交的直线。更具体来说，将两点0=(0,0,0)和n₂=(nx₂,ny₂,nz₂)分别投影到π₁ (0) 和π₁ (n₂) 上。投影到π₁上的直线是L1: Q(t) = π₁ (0) + tπ₁(n₂)，它和π₂的相交线能被计算出来。在最有效的情况下，也就是当n₁和n₂ 都为单位法向量并且常数p₁(0) 被预先存储起来的情况下，整个运算包括17次相加运算和22次相乘运算。

（C）3平面相交于一点。当法向量n₃ = n₁×n₂和d₃=0 (意味着通过原点)时，可以选择用隐式方程式表达的第三个平面π₃。这一直成立因为：(1) L垂直于π₃这样就和π₃相交，(2) 向量n₁，n₂和n₃线性无关。也就是说平面π₁，π₂和π₃相交于唯一点P₀，P₀必然也在L上。当π₃上的d3=0时，用3平面相交线的方程式，我们可以得出：

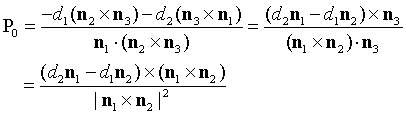
还有L的参数方程：

.

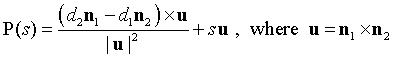这次求解共有11次相加和23次相乘。

当n₁和n₂为单位法向量且n₁ · n₂ = cos q（q是两向量之间的夹角）时，这个方程式可以被简化。然后，n₁ · n₁ = n₂ · n₂ = 1，和|n₁×n₂|² = sin² q = 1 – cos² q = 1 – (n₁ · n₂)² 作为它的分母。最终，我们利用叉乘的右结合性，对于任意的3D向量a，b，和c，等式a×(b×c) = (a· c)b – (a· b)c始终成立。应用到分子上，经过简化可以得出：(d₂n₁–d₁n₂)×(n₁×n₂) = (d₂ cos q – d₁) n₁ + (d₁ cos q – d₂) n₂。于是，

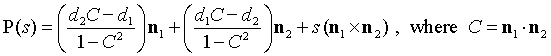
这种解决方案描述了L上的点P₀作为向量n₁和n₂的线性组合，这是通过原点的平面p₃的基础生产算法。运算次数为11次相加+20次相乘。

最后要说的一点是，最有效率的解决方法是解决方法(A)，这种方法计算出相交线的方程只用到了5次相加和12次相乘。

三平面相交

在3D中，三平面p1，p2 和p3有几下几种方式能够相交（或者不想交）：

几何关系	交集		数学表达
三平面平行			nj×nk=0 （j,k=1,3）
三平面相交	一个平面		n1·V1=n1·V2=n1·V3
三平面不相交	无		n1·V1¹n1·V2¹n1·V3¹n1·V1
只有两个平面平行，第三个平面和其余的两个平面分别相交于一条直线 [注：两个平行的平面有可能相交]	2条平行的直线 [重合部分 => 1 条直线]		只有当nj×nk=0 （j¹k）成立
没有两个平面平行，它们两两相交于三条直线。			nj×nk¹0 （j¹k）
相交线互相平行			n1·(n2×n3)=0
相交线相交	1条直线		从一条直线上测试一点
相交线不想交	3条平行的直线
相交线都不平行	一个特定的点		n1·(n2×n3)¹0

如图所示：

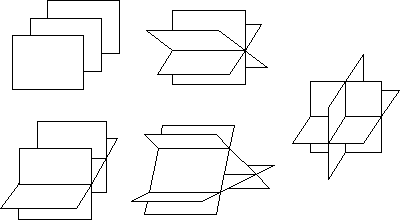
应该首先测试相交点的最普遍的情况，也就是说n₁·(n₂×n₃)¹0，它可以排除其它的情况。当相交点是一个特定点时，它由以下公式给出：

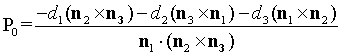
可以通过P₀是否满足p₁，p₂ 和p₃的参数方程来验证。

然而，当分母n₁·(n₂×n₃)非常小时，在计算性能上存在问题。在这种情况下，最好的办法是取其中两个平面的相交线，然后计算这条直线和第三个平面的相交点。

程序实现

//    Point and Vector with
//        coordinates {float x, y, z;}
//        operators for:
//            == to test equality
//            != to test inequality
//            Point  = Point ± Vector
//            Vector = Point - Point
//            Vector = Scalar * Vector    (scalar product)
//            Vector = Vector * Vector    (3D cross product)
//    直线、射线和线段由点定义{Point P0, P1;}
//        (直线是无穷的，射线和线段开始于P0)
//        (射线从P1向外延伸，但是线段结束于P1)
//    平面由一个点和一个方向向量定义{Point V0; Vector n;}
//===============================================================
#define SMALL_NUM  0.00000001 // anything that avoids division overflow
// 点乘(3D)
#define dot(u,v)   ((u).x * (v).x + (u).y * (v).y + (u).z * (v).z)
#define perp(u,v)  ((u).x * (v).y - (u).y * (v).x)  //正交运算(2D)

// intersect2D_2Segments():2D有限线段相交
//   输入：两条有限线段S1和S2
//   输出: *I0 = 相交点(如果存在)
//            *I1 = 相交线段的终点 [I0,I1] (如果存在)
//   返回值: 0=disjoint (no intersect)
//          1=intersect in unique point I0
//          2=overlap in segment from I0 to I1
int
intersect2D_Segments( Segment S1, Segment S2, Point* I0, Point* I1 )
{
    Vector    u = S1.P1 - S1.P0;
    Vector    v = S2.P1 - S2.P0;
    Vector    w = S1.P0 - S2.P0;
    float     D = perp(u,v);
    // 验证是否平行(包含一个点的情况)
    if (fabs(D) < SMALL_NUM) { // S1 和 S2 平行 if (perp(u,w) != 0 || perp(v,w) != 0) { return 0; // 不共线 } // they are collinear or degenerate // check if they are degenerate points float du = dot(u,u); float dv = dot(v,v); if (du==0 && dv==0) { // 线段点集 if (S1.P0 != S2.P0) // 在特殊点上 return 0; *I0 = S1.P0; // 在相同点上 return 1; } if (du==0) { // S1 作为一个单独的点 if (inSegment(S1.P0, S2) == 0) // 不在 S2上 return 0; *I0 = S1.P0; return 1; } if (dv==0) { // S2 作为一个单独的点 if (inSegment(S2.P0, S1) == 0) // 不在 S1上 return 0; *I0 = S2.P0; return 1; } // 它们为共线线段 – 部分重叠 (或者不重叠) float t0, t1; Vector w2 = S1.P1 - S2.P0; if (v.x != 0) { t0 = w.x / v.x; t1 = w2.x / v.x; } else { t0 = w.y / v.y; t1 = w2.y / v.y; } if (t0 > t1) {                  // t0 必须比 t1小
                float t=t0; t0=t1; t1=t;    // 如果t0 不比 t1小就交换
        }
        if (t0 > 1 || t1 < 0) {
            return 0;     // 不重叠
        }
        t0 = t0<0? 0 : t0; // 控制最小值为 0 t1 = t1>1? 1 : t1;              // 控制最大值为 1
        if (t0 == t1) {                 // 交集是一个点
            *I0 = S2.P0 + t0 * v;
            return 1;
        }

        // 在有效子线段内部分重叠
        *I0 = S2.P0 + t0 * v;
        *I1 = S2.P0 + t1 * v;
        return 2;
    }

    // 线段倾斜，可能相交于一点
    // 取得S1的相交参数
    float     sI = perp(v,w) / D;
    if (sI < 0 || sI > 1)               // 和 S1没有相交
        return 0;
    // get the intersect parameter for S2
    float     tI = perp(u,w) / D;
    if (tI < 0 || tI > 1)               // 和 S2没有相交
        return 0;
    *I0 = S1.P0 + sI * u;               // 计算 S1 的相交点
    return 1;
}
//===============================================================
// inSegment(): 验证点是否在线段内
//    输入:  a point P, and a collinear segment S
//    返回值: 1 = P is inside S
//            0 = P is not inside S
int
inSegment( Point P, Segment S)
{
    if (S.P0.x != S.P1.x) {    // S is not vertical
        if (S.P0.x <= P.x && P.x <= S.P1.x) return 1; if (S.P0.x >= P.x && P.x >= S.P1.x)
            return 1;
    }
    else {    // S is vertical, so test y coordinate
        if (S.P0.y <= P.y && P.y <= S.P1.y) return 1; if (S.P0.y >= P.y && P.y >= S.P1.y)
            return 1;
    }
    return 0;
}
//===============================================================
// intersect3D_SegmentPlane(): 线段和平面相交
//    Input:  S = a segment, and Pn = a plane = {Point V0; Vector n;}
//    Output: *I0 = the intersect point (when it exists)
//    Return: 0 = disjoint (no intersection)
//            1 = intersection in the unique point *I0
//            2 = the segment lies in the plane
int
intersect3D_SegmentPlane( Segment S, Plane Pn, Point* I )
{
    Vector    u = S.P1 - S.P0;
    Vector    w = S.P0 - Pn.V0;

    float     D = dot(Pn.n, u);
    float     N = -dot(Pn.n, w);

    if (fabs(D) < SMALL_NUM) {          // 线段和平面平行
        if (N == 0)                     // 线段在平面内
            return 2;
        else
            return 0;                   // 没有交集
    }
    // they are not parallel
    // compute intersect param
    float sI = N / D;
    if (sI < 0 || sI > 1)
        return 0;                       // 没有交集

    *I = S.P0 + sI * u;                 // 计算线段的相交点
    return 1;
}
//===============================================================
// intersect3D_2Planes(): 两平面相交
//    Input:  two planes Pn1 and Pn2
//    Output: *L = the intersection line (when it exists)
//    Return: 0 = disjoint (no intersection)
//            1 = the two planes coincide
//            2 = intersection in the unique line *L
int
intersect3D_2Planes( Plane Pn1, Plane Pn2, Line* L )
{
    Vector   u = Pn1.n * Pn2.n;         // 叉乘
    float    ax = (u.x >= 0 ? u.x : -u.x);
    float    ay = (u.y >= 0 ? u.y : -u.y);
    float    az = (u.z >= 0 ? u.z : -u.z);

    // test if the two planes are parallel
    if ((ax+ay+az) < SMALL_NUM) { // Pn1 和 Pn2 近似平行 // test if disjoint or coincide Vector v = Pn2.V0 - Pn1.V0; if (dot(Pn1.n, v) == 0) // Pn2.V0 在 Pn1内 return 1; // Pn1 and Pn2 重合 else return 0; // Pn1 and Pn2 不相交 } // Pn1 和 Pn2 相交于一条直线 // 首先定义叉乘的最大坐标值 int maxc; // 最大坐标值 if (ax > ay) {
        if (ax > az)
             maxc = 1;
        else maxc = 3;
    }
    else {
        if (ay > az)
             maxc = 2;
        else maxc = 3;
    }

    // 接下来，取得相交线上的一点
    // 将最大值置为0，求解出另外两个值
    Point    iP;               // 相交点
    float    d1, d2;           // 两个平面方程中的常数
    d1 = -dot(Pn1.n, Pn1.V0);  // 注: 事先在平面内定义
    d2 = -dot(Pn2.n, Pn2.V0);  // 同上

    switch (maxc) {            // 选择最大坐标
    case 1:                    // 相交于 x=0
        iP.x = 0;
        iP.y = (d2*Pn1.n.z - d1*Pn2.n.z) / u.x;
        iP.z = (d1*Pn2.n.y - d2*Pn1.n.y) / u.x;
        break;
    case 2:                    // 相交于 y=0
        iP.x = (d1*Pn2.n.z - d2*Pn1.n.z) / u.y;
        iP.y = 0;
        iP.z = (d2*Pn1.n.x - d1*Pn2.n.x) / u.y;
        break;
    case 3:                    // 相交于 z=0
        iP.x = (d2*Pn1.n.y - d1*Pn2.n.y) / u.z;
        iP.y = (d1*Pn2.n.x - d2*Pn1.n.x) / u.z;
        iP.z = 0;
    }
    L->P0 = iP;
    L->P1 = iP + u;
    return 2;
}
//===============================================================

参考文献

Foley, van Dam, Feiner & Hughes, 计算机图形学( C语言第二版), 3.12节 “线裁减” (1996)
Francis Hill, “正交点乘运算的乐趣” in 图形几何IV (1994)
Michael Mortenson, 计算机图形学手册: 几何和数学 (1990)
Joseph O’Rourke, 基于C的计算几何(第二版), 第7章 “查询和相交” (1998)

转载请注明：陈童的博客 » 计算几何算法5. 直线、线段和平面相交（2D和3D）