描述统计
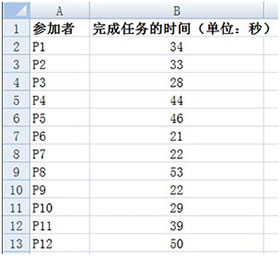
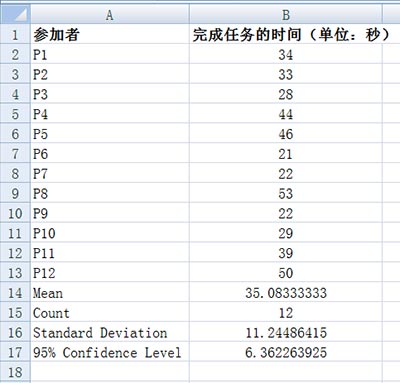
描述统计(descriptive statistics)对任何等距或比率数据来说是都是基本的。顾名思义,描述统计仅对数据进行描述而不对较大群体进行任何推论。而推论统计可以对一个远大于样本的较大群体提出一些结论或推论。利用大多数统计软件包都能够非常容易地对描述统计进行计算。例如下表列出了在一个可用性研究中,12名被试者完成任务的时间(单位:秒)
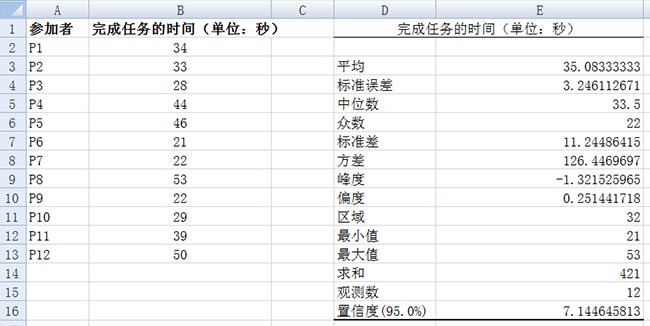
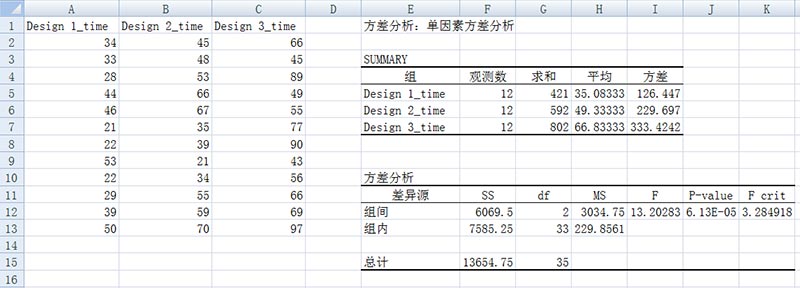
Excel中的数据–>数据分析结果:
1. 集中趋势的度量
当进行描述统计时.集中趋势(Central tendency)是首先需要查看的统计。简单来说。集中趋势就是任何分布的中间或中央部分。最常见的三种集中趋势的测量是平均数、中数(Median)和众数(Mode)。
中数是数据分布的中点,一半的参加者低于中数,一半的参加者高于中数。众数是原始数据中最常出现的数值。
2. 变异性的度量
变异性测量(Measures of variability)显示数据总体中数据的分散或离散程度。数据的变异性或离散程度越大,通过这些数据了解全体的可靠性程度就越低;变异性或离散程度越低,将样本的结果推论到全体的置信度就越大。三种最常见的变异程度测量指标为:全距(range)、方差(variance)、标准差(standard deviation)
全距是最小数据点与最大数据点之间的距离。
方差是另一种常见且重要的变异性测量。它说明了数据相对于平均数或均值的离散程度。计算方差的公式:首先求各数据与平均数的差,然后求其平方,得到的值再求和二后用样本数t减1之后的差值去除该求和之后的结果。
标准差就是方差的平方根。
3. 置信区间
置信区间对任何可用性专业人员来说都是极具价值的。置信区间是一个范围。用来估计某统计值的总体实际值。例如,假设需要估计整个总体的平均数,且希望估计正确的概率达到95%,下图中的计算结果是7秒左右,这意味着可以确信有95%的概率总体平均数为35±7,即28秒-42秒。
Excel的“Confidence”函数可以计算置信区间,公式如下:
=confidence(a系数, 标准差, 样本大小)
a系数的典型值是5%或0.05,标准差可以通过Excel的“stdev”函数计算,样本大小通过“count”函数获得。
比较平均数
比较平均数有多种方法,但是,在进行统计之前,应该首先回答以下问题:
(1)是同一组参加者内的比较还是不同参加者组之间的比较?例如,如果比较来自于男性和女性参加者的数据,这很可能是不同参加者组之间的比较。像这样比较的不同样本被称为独立样本(independent samples)。但是,如果比较的是同一组参加者在两种不同产品或设计上的数据(组内设计,within-subjects design)。则需使用重复测量分析或配对样本(paired samples)比较。
(2)样本量有多大,如果样本量小于30,可以使用t检验;如果样本量等于或大于30,则使用z检验。
(3)有多少样本需要进行比较?如果比较的是两个样本,可以使用t检验;如果比较三个或更多的样本,则使用方差分析(也叫做ANOVA)
1. 独立样本
在可用性研究中,将经常会比较基于独立样本的平均数。这仅仅意味着这些组别是不同的。例如,感兴趣的是在满意度评价中专家级参加者与新手参加者之间的比较。最常见的问题是检验这两个群体是否存在差异。这种比较在Excel中可以轻松地实现。
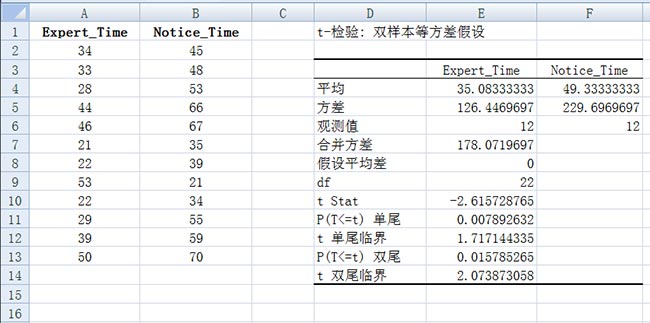
t-检验: 双样本等方差假设
可以看出双尾分布的p值约为0.016,小于0.05的阈值。因此,可以得出专家和新手的完成时间在0.05水平上具有统计意义上的显著差异。
2. 配对样本
当要比较同一组参加者的平均数时,应使用配对样本(paired samples)t检验.例如,感兴趣的是两个原型设计之间是否存在差异。假如让同一组参加者先使用原型A完成任务、然后再使用原型B完成类似的任务。并且测量的变量是主观报告的易用程度和时间,则使用配对样本t检验。
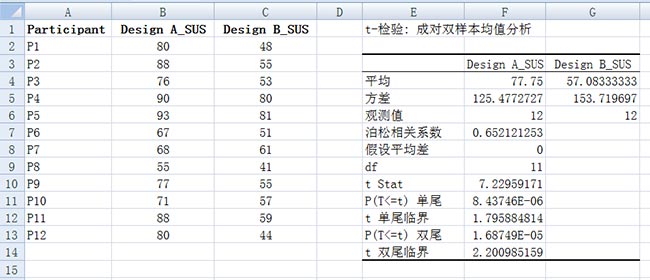
t检验:平均值的成对二样本分析
3. 比较两个以上的样本
不总是只比较两个样本,有时候想要比较的不同样本是三个、四个甚至六个。这时可以使用方差分析(通常叫做(ANOVA)能够确定两个以上的组别之间是否具有显著的差异。
结果包括两个部分。设计3的平均完成时间明显较长,而设计1的完成时间较短。设计3的方差比较大,而设计1的方差较小。
结果的第二部分说明了差异是否显著。F值等于13.20,而达到显著水平的相应临界值为2.8,p值为0.00006表明了结果的统计显著性。完全地理解结果所表示的含义是重要的:
结果表明“设计”这一变量效应显著。这一结果不一定表示每种设计的均值都与其他各种设计的均值之间都有显著差异,它仅仅表示总的效应是显著的。为了要看任意一对平均数之间是否有显著差异,可以对两组数值进行两样本t-检验。
变量之间的关系
有时候,知道不同变量之间的关系是很重要的。例如,有些人第一次观察可用性测试时就会注意到,参加者所说的和所做的并不总是一致的。很多参加者使用原型完成任务会很费力,但是,当要求他们评价原型的易用程度时。他们经常会给予其很好的评价。
相关
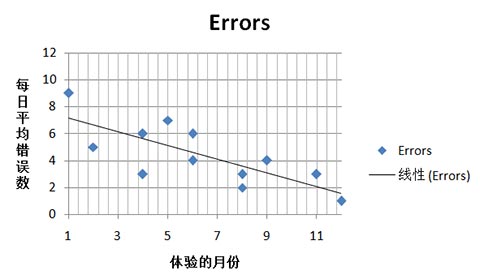
开始检验两个变量之间的关系时,可以通过两点变量的散点图观察可视化后的样子。下面的散点图表示了体验的天数(x轴)与每日平均错误数(y轴)之间的关系。随着产品体验的逐月增加,每日平均错误书逐渐减少,这种关系称为负相关。这条贯穿的直线称为趋势线(Trend line)
还可以通过“Correlation”函数来计算相关系数。
转载请注明:陈童的博客 » 可用性研究中的描述统计